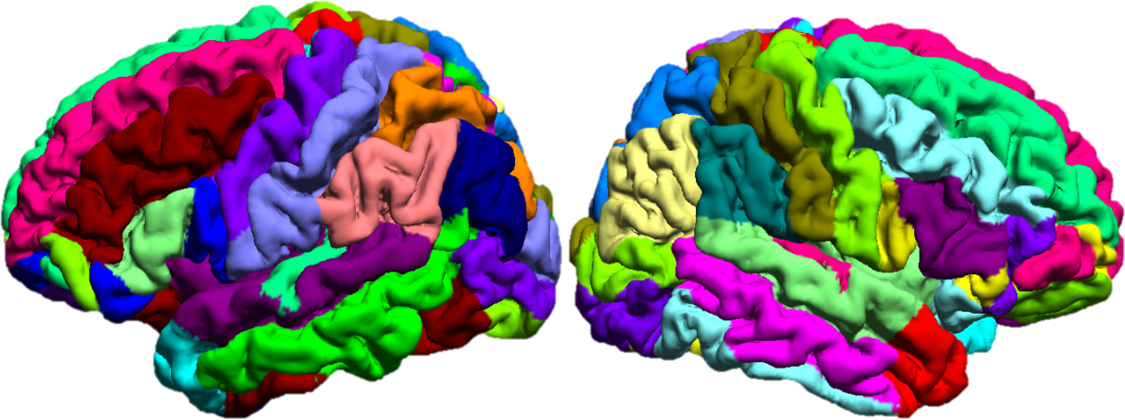
SVReg: Technical Details
Automated Spatial Alignment and Labeling
The second component of BrainSuite’s analysis sequence produces spatial alignment between two subjects using the surface models and label volumes identified using the brain segmentation and surface extraction methods. This process, summarized below, can align both the surface models and the volumes interior to them.
Curvature Representation and Surface Smoothing: The surface alignment procedure takes as input surface mesh models that represent two brains (subject and atlas) that are extracted from 3D MRI data using the methods above. For this stage, BrainSuite use a medial cortical surface mesh, which is computed based on the inner and outer boundaries. This mesh has a 1-1 mapping to the inner and outer meshes. The first step is to smooth these surfaces iteratively using mean curvature flow. The computed mean curvature is also used in later steps as a feature for surface matching. The mean curvature is used as it represents the sulci fundi with negative values and gyral crowns with positive values; therefore its alignment leads to accurate alignment of the cortex (Joshi et al., 2012).
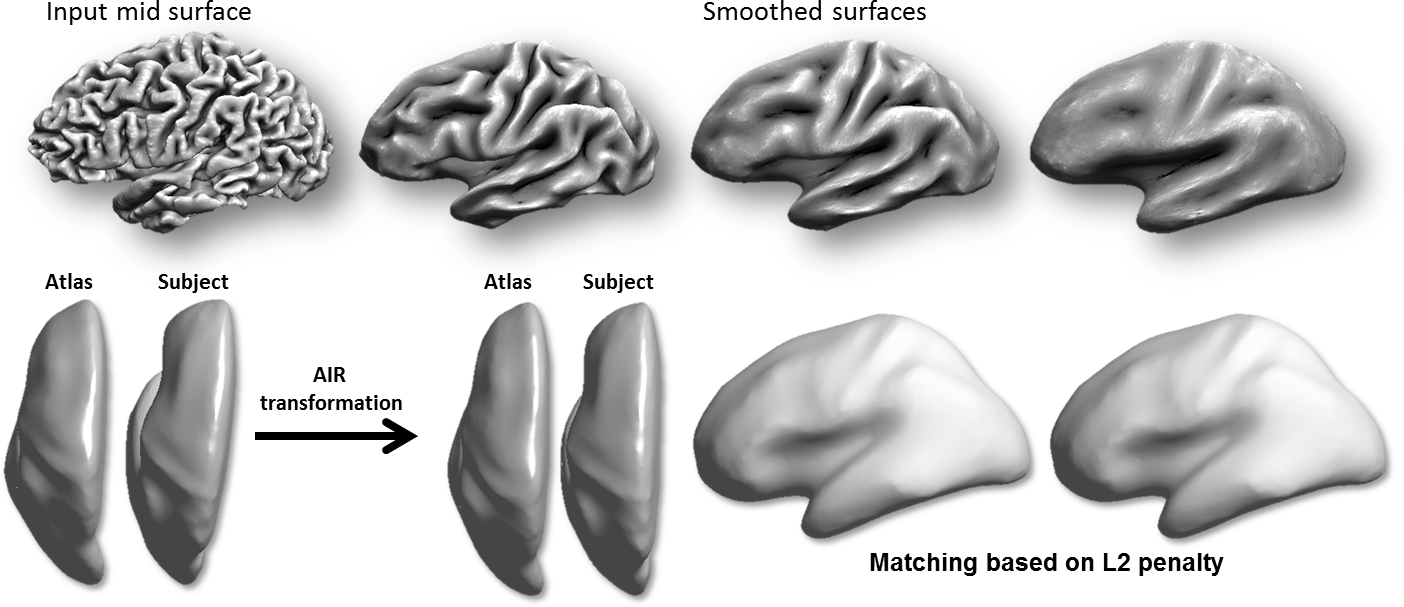
Coarse Alignment of Smoothed Surfaces: These smoothed surfaces are then aligned in 3D space. First a 5th order polynomial warping field is applied to the surfaces using AIR. This is then followed by a L2-energy-based surface registration procedure. This coarse alignment step is fast, as it is performed in 3D rather than flat space, and aligns the major lobes, which are better defined by their 3D location than local features (Joshi et al., 2012).
Surface Parameterization: Next, each hemisphere is mapped to the unit square using a parameterization process that minimizes the p-th norm of the elastic energy in the surface (Joshi et al., 2005). The p-harmonic maps generate a one-to-one correspondence between a unit square and the cortical surfaces such that the inter-hemispherical fissure dividing the left and right hemispheres is mapped to the edges of the unit square. The curvature maps generated in the previous steps are then transferred to the unit square using the point correspondence established by these p-harmonic maps (Joshi et al., 2012).
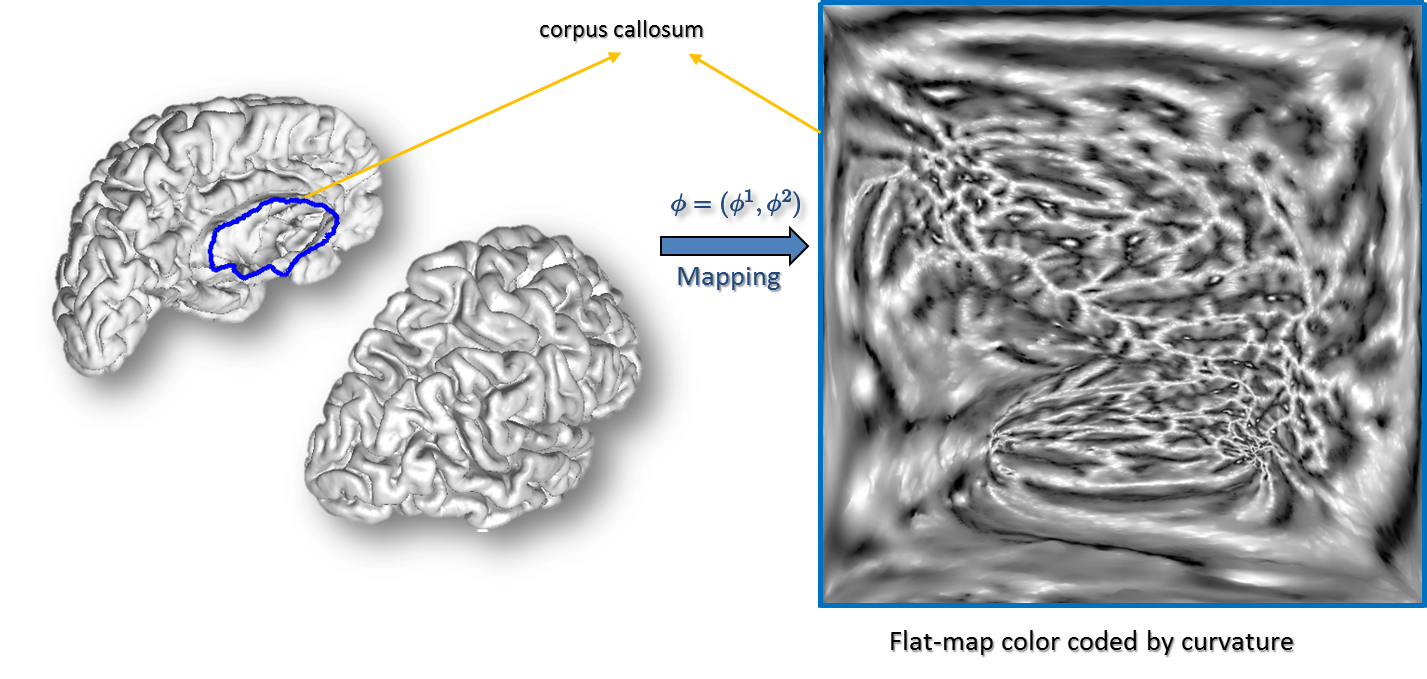
Curvature-Based Alignment: To perform the curvature based alignment, the brain surface is modeled as an elastic sheet and the associated linear elastic equilibrium equation is solved using the Finite Element Method (FEM). The alignment of the curvature maps is then performed by minimizing the cost function—a weighted sum of a curvature matching penalty and a 3D coordinate matching penalty, regularized by an elastic energy. This minimization is performed by applying the L-BFGS optimization scheme. After performing the atlas to subject registration, the sulcal curves and cortical labels from the atlas are applied to the subject’s cortical surface (Joshi et al., 2012).

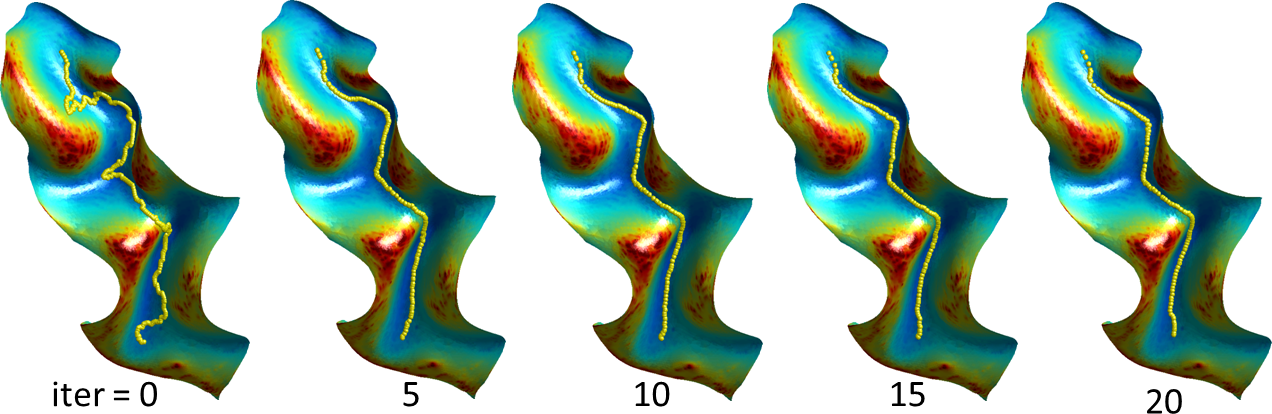
Refinement: Refinement of the labels and sulcal curves is performed using a level-set method. Typically, when the sulcal curves are transferred from the atlas to the subject surface, they are in the correct sulcal valley but not aligned correctly to its lowest point. To reduce the computational burden, a small surface patch is calculated around the sulcus of interest using front propagation. The sulcal curve is then used as the zero set of an unknown function, and the curve’s length is minimized, weighted by a sigmoid of the curvature of the surface it is embedded in. The resulting system of equations from this energy minimization problem is solved for the function (and thus the curve) subject to these bounds using a preconditioned conjugate gradient method with a Jacobi preconditioner (Joshi et al., 2012). A similar procedure is used to refine the label boundaries between adjacent ROIs, with the surface of the two ROIs replacing the surface patch and the boundary between the ROIs replacing the sulcal curve.
Harmonic Extension: We perform volumetric spatial alignment of brains by extending the surface registration to the entire volume (Joshi et al., 2009; Joshi et al., 2007). This begins with two surfaces that have been aligned using the process described in Steps 1 through 5. For each brain, the unit-square representations of the brain surfaces are mapped onto the unit sphere. The interior brain volume is then mapped to the unit ball. This is achieved by extrapolating from the surface to the interior of the sphere while minimizing the harmonic energy of the map from brain to sphere. This harmonic mapping gives one-to-one correspondence between the two brains based on their respective maps to the unit sphere. This provides an initial registration based solely on the initial alignment of cortical geometry.

Extension to Whole Volume: The deformation d(x) inside the dewisp-mask and at the pial surface is constrained to be the deformation found using harmonic mapping to the unit ball. We carved out an area around hippocampus and ventricles from the white matter mask on the atlas brain and transfer this to subject using AIR deformation map. This area is defined through hippo_carved mask file in the atlas directory. The hippo carved mask area is shown in the figure below using green outline.
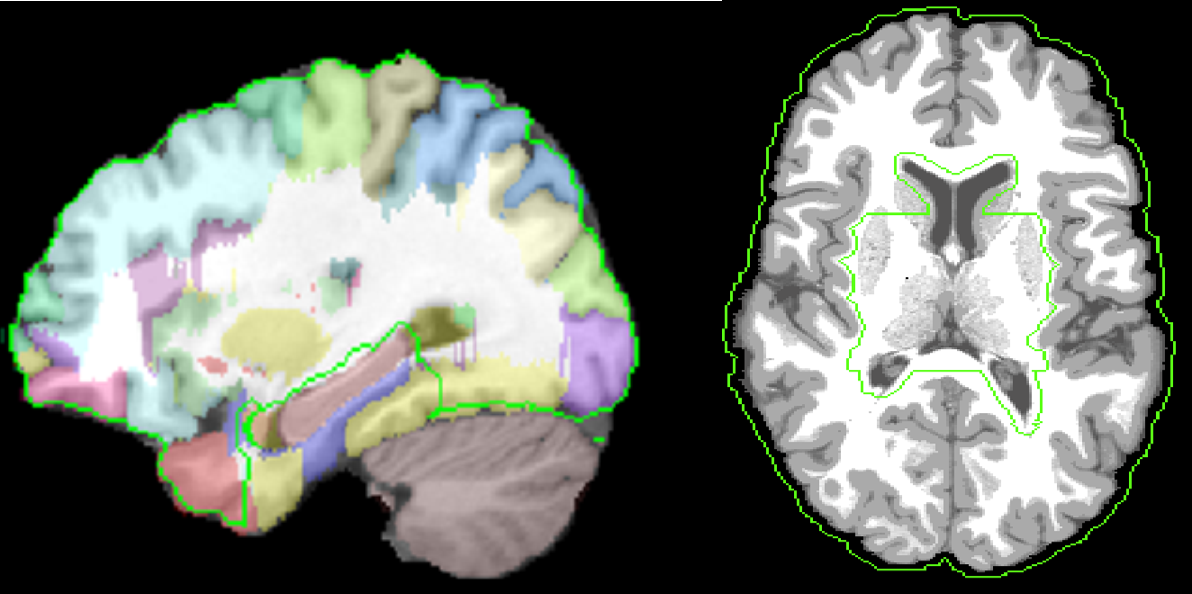
One deformation is found by computing an AIR registration that was computed from subject to intermediate atlas in BrainSuite, as well as inverse of svreg atlas to the intermediate BrainSuite atlas between pial surfaces of subject and atlas surface coordinates. Using these two constraints, the Laplacian cost is minimized for the whole 3D volume. This results in extension of the deformation from dewisp mask surface to the rest of the brain. Negative Jacobian Fixing is performed by computing pseudo-inverse of the deformation field by repeatedly inverting the deformation field.
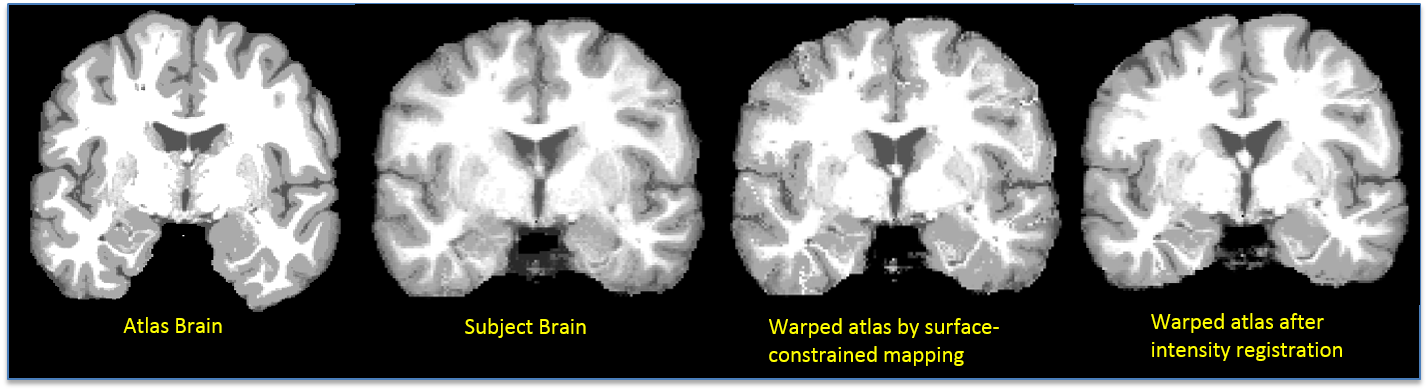
Intensity Registration: The harmonic extension ensures that cortical features will be aligned. However, since the interior mapping is based solely on geometry of the cortex, subcortical features will tend to be misaligned. Thus, a refinement of this mapping is computed by minimizing the elastic bending energy driven by an intensity matching force. As with surface registration, covariant derivatives are used to ensure the deformation is computed with respect to the intrinsic geometry of the brain. The intermediate sphere allows a flow from one cortical surface to the other, subject to any sulcal matching constraints. The output of this process is a point correspondence between the two brain volumes based on the deformation required to map one to the other. The cortical constraint ensures that one cortical surface maps precisely onto the other (Joshi et al., 2007). Once the atlas volume is registered to the subject’s volume, the atlas’ warped label volume acts as a label volume for the subject. Inverse of the deformation map is also computed and stored. The following figure shows result of surface-constrained registration and intensity registration. An improvement in matching of ventricles can be seen in the figure below.
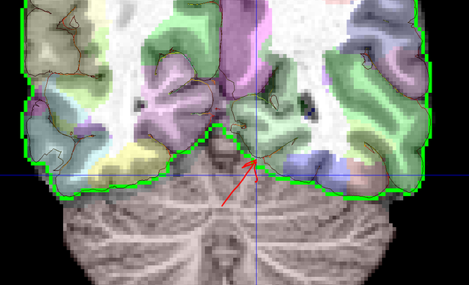
Label Refinement: In order to counter the effects of nearest neighbor interpolation and to make the label boundaries smoother, a median filerting with 3x3x3 kernel is performed. Additionally, a connected compument analysis is performed to remove isolated voxels which could result due to similar issues in the atlas or non-invertible deformation at a few points. The cortical labels are constrained by a mask defined by pial surface-based mask. Third ventricle is allowed to lie both inside and outside the cortical mask. The figure below shows the mask defined by pial surface and cerebrum mask. The regions such as brainstem and cerebellum are constrained to lie outside the mask. A mask for these regions was generated by labels transferred from surface registration extension and dilating those label boundaries. The figure below shows cerebrum mask as a green curve and pial surface as a dark curve. The red arrow shows one region where pial surface based mask can help in better constraining the cortical labels.
The current version of the registration software is implemented in Matlab, and comes with two manually-labeled single-subject template and inner, mid, and pial cortical surfaces carefully extracted and hand-labelled by an expert neuroanatomist.