Spatial alignment
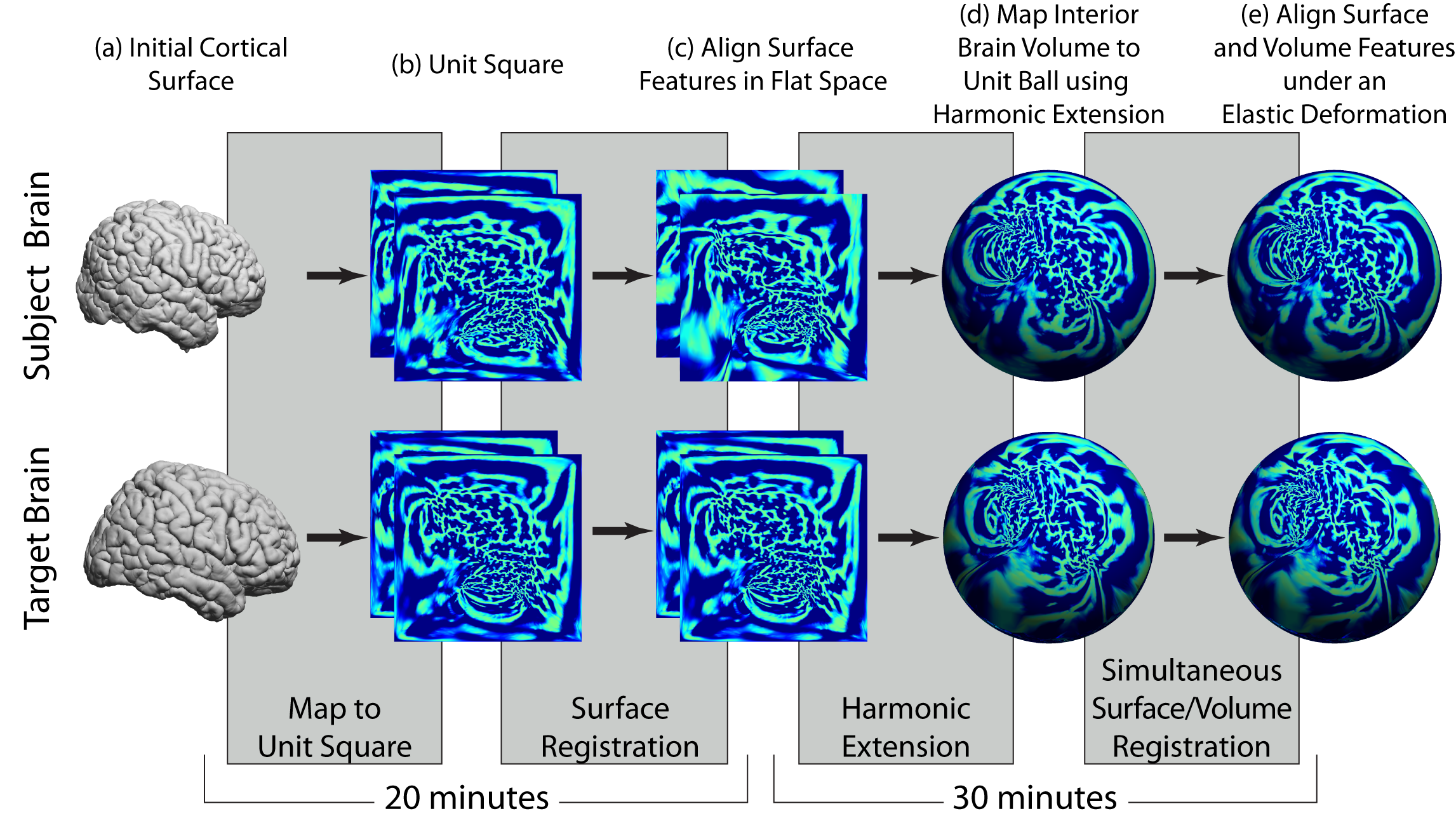
The second component of our analysis sequence produces spatial alignment between two subjects using the surface models and label volumes identified using our brain segmentation and surface extraction methods. As illustrated in the figure above, this process can align both the surface models and the volumes interior to them. The process is summarized below.
- Surface parameterization: Our surface alignment procedure takes as input surface mesh models that represent two brains (subject and target/atlas) that are extracted from 3D MRI data using the methods above. For this stage, we use a medial cortical surface mesh, which is computed based on the inner and outer boundaries. Again, this mesh has a 1-1 mapping to the inner and outer meshes. We map each hemisphere to the unit square using a parameterization process that minimizes the p-th norm of the elastic energy in the surface (Joshi et al., 2005).
- Feature alignment: The parameterization process will optionally take as input landmark curves traced on the brain surfaces (e.g., sulcal curves); when present, these are used to deform the surfaces with respect to the 2D flat space such that the landmarks are aligned. Following the initial flattening, the registration procedure aligns the maps further by matching curvature features from each brain surface. During these alignment procedures, the deformation is computed to minimize a linear elastic bending energy. Computation of this deformation uses a weighting function based on the Jacobian of the flat maps to minimize the effect of metric distortion that occurs during the flat mappings. The output of the surface registration module is a one-to-one map between the two cortical surfaces. This makes the registration result independent of the specific parameterization used. The output of the surface registration module is a one-to-one map between the two cortical surfaces.
- Harmonic Extension: We perform volumetric spatial alignment of brains by extending the surface registration to the entire volume (Joshi et al., 2009a; Joshi et al., 2007c). This begins with two surfaces that have been aligned using the process described in Steps 1 and 2. For each brain, we map the unit-square representations of the brain surfaces onto the unit sphere. We then map the interior brain volume to the unit ball. This is achieved by extrapolating from the surface to the interior of the sphere while minimizing the harmonic energy of the map from brain to sphere. This harmonic mapping gives one-to-one correspondence between the two brains based on their respective maps to the unit sphere. This provides an initial registration based solely on the initial alignment of cortical geometry.
- Elastic Deformation: The harmonic extension ensures that cortical features will be aligned. However, since the interior mapping is based solely on geometry of the cortex, subcortical features will tend to be misaligned. We thus compute a refinement of this mapping by minimizing the elastic bending energy driven by an intensity matching force. As with surface registration, we use covariant derivatives to ensure the deformation is computed with respect to the intrinsic geometry of the brain. The intermediate sphere allows us to flow one cortical surface with respect to the other, subject to any sulcal matching constraints. The intermediate sphere allows us to flow one cortical surface with respect to the other, subject to any sulcal matching constraints. The output of this process is a point correspondence between the two brain volumes based on the deformation required to map one to the other. Using the cortical constraint, we ensure that one cortical surface maps precisely onto the other (Joshi et al., 2007c).
- Brain Labeling: If the target brain is a labeled atlas, then we can resample the label data onto the subject model. This includes both surface and volume labels. We use an atlas developed by neuroanatomy experts that provides labels for 100 brain regions.
Our current version of the registration software is implemented in Matlab, and uses a cost function that controls four aspects of the registration warp: (1) intensity matching of the interior brain volumes; (2) curvature matching of the cortical surfaces; (3) smoothness of the deformation; and (4) non-negativity of the Jacobian maps to ensure that the transformation is one-to-one. The cost function is discretized over a tetrahedral mesh using finite elements; this mesh is generated using TetGen (http://tetgen.berlios.de/), an open source tetrahedral mesh generator.